New Criticals

In this post I’d like to begin shifting focus from general thermodynamic considerations to a more detailed discussion of the emergence of life, but let’s begin with an overview of how the laws of thermodynamics both constrain and enable the possibilities of living organizations.

Some jargon: A living organism is an informed, autocatalytic, non-equilibrium organization. Each of these words expresses specific enabling constraints related to the conditions of energy flow through organisms. In this post I treat the catalytic and the non-equilibrium aspects and briefly introduce the concept of information. The next post will discuss more detailed aspects of information and complexity, as well as the meaning of autocatalysis (self-making). But we begin with the most central concept: an organism is a non-equilibrium organization.

What this expresses is the simple fact that any living system is in a higher energy state than the corresponding material in a non-living state would be. Simply put, you are hotter than the room, and one really crude way of telling how long someone has been dead is to check their temperature. So we have an intuition that life depends on the maintenance of this higher energy state, and our experience first reveals this dependence to us a constraint: We have to keep eating and breathing and we have to stay warm. To understand why, however, we have to understand what this constraint enables: All non-equilibrium distributions of matter are to some extent more organized than the corresponding equilibrium distribution would be. This is the converse of the classical version of the second law. Our classical understanding of entropy was based on the fact that the microscopically random motions of heat flow cannot ever be completely converted into directed motion, which we call “work.” So it basically said that no process can be 100% efficient. Well for exactly the same statistical reasons, no process can be 100% inefficient either. You can’t have heat flow through a system without, at the very least, having higher average kinetic energies near the source (hot thing) than the sink (cold thing). This idea comes from H. J. Hamilton.

When thinking about steam engines, it never occurred to anyone that this fact had any significance. Who cares that you can’t be 100% wasteful with your precious, precious coal? But it has enormous significance for the emergence of life, because it says that energy flows through a system must, to some extent, organize that system. The first book to my knowledge to explicitly treat this topic was Harold Morowitz’s “Energy Flow in Biology.” One slightly subtle point that people often miss: it is not energy per se that organizes a system, but energy flow. Life occurs between a source and a sink, and what it requires is not any absolute amount of energy but an energy difference which we call a gradient. It is the energy gradient that causes the spontaneous flow of energy from the source to the sink, and it is the existence of the flow that is the source of the organization. Or rather, a directed flow is an organization. Might not be much of an organization compared to the circulatory and nervous systems, but a river is, in this sense, “organized.” It is obvious that the water molecules in a river are not moving randomly with respect to one another but are moving together in response to the direction of the flow. The flow is occurring as a way of dissipating gravitational potential. This idea was mathematically formalized by Ilya Prigogine with the concept of a dissipative structure. So another way of saying that life is a non-equilibrium organization is to say that organisms are a class of dissipative structures.

Being a dissipative structure implies some formal criteria for the entropy production of a system.  Remember that the second law says that irreversible processes must always be accompanied by an increase in entropy. For an isolated system that cannot exchange matter or energy with its surroundings, this results in the boring prediction that the system will evolve into the state with the highest possible entropy and then do nothing. For an open system, however, which is capable of exchanging matter and energy with its environment, we may split the entropy change term into one term representing the entropy change as a result of processes internal to the system and another term representing the entropy change as a result of flows into and out of the system, like so:

∆S = ∆Si + ∆Se

The second law requires that ∆Si, the entropy change due to irreversible processes internal to the system, be positive. It is thus a measure of the energetic cost of maintaining a particular non-equilibrium organization. But the second law places no constraint on the sign of ∆Se, the term for the entropy exchanged with the environment. Schrodinger’s “What is life?” (1944) is generally considered to be the first modern work of biophysics, and it contains a number of vague insights which provided the basis for the mathematical formalization of these ideas in the work of Prigogine and Morowitz. Schrodinger understood that life could not be violating the second law, despite naive appearances, but the connections between entropy and organization were far from understood at this point. Schrodinger knew, however, that the act of eating and breathing was a way of “concentrating a stream of order", or "negative entropy” upon the organism.

So for any system that can exchange matter or energy with its surroundings, the possibility arises that ∆Se is negative and greater in magnitude than ∆Si, rendering the overall entropy change of the system negative. Such a system will be spontaneously driven into higher energy states by flows of matter and energy seeking to dissipate the potential difference between the external source and sink. These dissipative flows through the system represent its internal organization. So that’s what is meant by the term “non-equilibrium organization.” We will revisit this topic when we discuss the chemistry of eating and breathing (oxidative phosphorylation) in depth.

So that’s how the laws of thermo act as an enabling constraint on the energetic conditions necessary for life. But I said that organisms are a class of dissipative structure, not just any old dissipative structure. Any material kinetically responding to an energy gradient is dissipative to some extent, but most systems exhibiting this property are not alive (streams, candles, stars, tornadoes and hurricanes...anytime you see an ensemble of matter moving together basically). Dissipative structuring is a necessary but insufficient condition for life. The second way in which the laws of thermo act as an enabling constraint for life involves the generation of molecular complexity to provide the basis for functional information which allows networks of dissipative flows to coalesce into autocatalytic cycles. So now lets start unpacking all that jargon.

If you recall my last post, then you know that chemical changes which result in a greater diversity of molecules always increase the number of available microscopic arrangements of the system, and thus they increase entropy. But nothing guarantees that an ensemble of matter can undergo chemical transformations, and if the chemistry is possible nothing guarantees that the energy input into the system is sufficient to drive the possible chemical changes. This is why being a dissipative structure is a necessary condition for life. In general, for a given set of chemical possibilities, there exists an upper and lower bound for the magnitude of the energy gradient required to direct those possibilities into stable pathways of dissipation. When people talk about “the goldilocks zone” for the distance between a planet and its star required to support life, what they are estimating is the range of temperature differences under which stable dissipative flows are possible with organic chemistry in water. I haven't said much about water yet but it is to intercellular processes what space is to the biosphere, so we'll get there soon.

So to assess the possibilities for producing configurational entropy, you need an idea of the possible number of molecules a given set of simpler molecules might form if provided access to a stable energy gradient. As we discussed last time, the possibilities for organic molecules are endless, and philosophy of biology literature is riddled with examples of simple calculations demonstrating ridiculous statistics, even if life made a new organic molecule every nanosecond it would take 1000 times the age of the universe to make them all and so on. So this aspect of configurational entropy production is an enabling factor for life: Given a stable external gradient and a basis set of molecules capable of being chemically rearranged, molecular complexity will spontaneously increase. Complexity (or just molecular variety if that’s less confusing) is the raw material for functional information but complexity and information are not synonymous. Information is molecular complexity coupled to a functional relationship with a dissipative flow. Life requires information, not just complexity. So the next question is “under what conditions can molecular complexity be utilized as functional information?”

To answer this question we must understand that pathways of dissipation are constrained by the chemical possibilities of a system. Imagine a pot of water on a stove. You heat it. The water molecules wiggle more vigorously. When they wiggle with more energy than the energy in the hydrogen bonds holding them together, they fly off into the gas phase and we say the water is boiling. The phase change occurs as a way of dissipating the energy input from the stove. Why doesn’t it do something more interesting? Because it’s just pure water and changing phase is the only thing it can do to dissipate potential. But if I have an ensemble of organic molecules in water, and maybe even with some oil around too, then it becomes more likely that the components of the system have more options for dissipation. Instead of a pure compound changing phase, the system can dissipate the input energy by doing some chemistry also. As molecular complexity increases, it becomes more and more likely that at least one molecule in the system is catalytic. This means that it will greatly accelerate the rate of one or more possible chemical reactions in the system.

Once a system possesses a catalytic capacity, it is no longer required to evolve deterministically to the lowest energy state it can occupy, because there is no guarantee that the process being catalyzed leads to the most stable configuration of the atoms involved. For a system with no catalytic properties, it is certain that its final state (which might take it a very long time to reach) will have the lowest internal energy possible and this corresponds to the system having dissipated as much potential as it possibly can.

But catalysis makes time relevant to the evolution of a system, because what really matters is not which processes lead to the most stable final state but rather which processes occur fastest. The fastest process always happens the most. As a result, it is now possible that the distribution of matter in the system becomes displaced from its equilibrium distribution. So the gradient alone provides the basis for the system having kinetic energies that are higher than their equilibrium values, and the catalytic properties of a system are the basis by which its material distribution can move away from equilibrium. This is all a little abstract, but concrete examples are chemically complicated so let me just show you a picture and I promise to discuss this in greater detail next time:

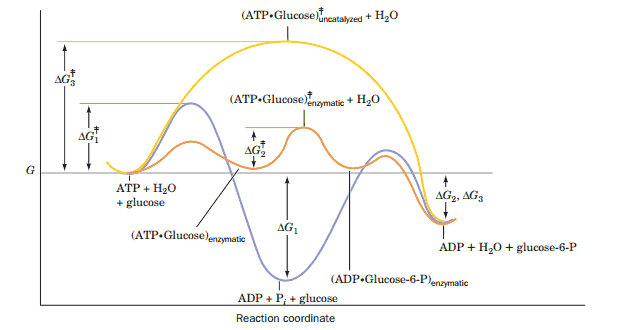
The chemical degradation of sugar (glucose) which provides energy for life processes begins when a protein catalytically attaches a phosphate ion to the sugar. Energy is on the y-axis and the progress of the reaction is on the x-axis. Each curve is tracking the energy of a different chemical process. The bottom curve, in blue, contains the lowest energy, equilibrium state of the system and corresponds to an unproductive dissociation of the phosphate ion into water. This won’t degrade the sugar and thus it won't help keep you alive, but it would be the thermodynamically favored outcome in the absence of the protein which catalyzes the reaction. The protein provides a template which lowers the activation energy required for putting the phosphate on the sugar. The activation energies are represented by the highest point on each curve, and that corresponds to the energy input required to make the process happen. You can see that the orange curve (protein catalyzed reaction) has the lowest activation energy even though the blue curve will proceed to a lower overall energy state. Lower activation energy, however, means that it's thousands or millions of times more likely that a random thermal fluctuation will be large enough to cause a reaction. This increased probability in turn leads to an accelerated reaction rate (thousands of times more likely to happen also means it occurs thousands of times more often), and practically all of the glucose ends up with a phosphate attached. The yellow curve represents the energy landscape for the uncatalyzed addition of phosphate to the sugar. You can see that its activation energy is very high, and consequently that without the protein there to catalyze the reaction this process would never occur.

Ok so hopefully we now have some intuition that catalysis is the basis for non-equilibrium distributions of matter, and that the likelihood of catalyzing a particular transformation increases as molecular complexity increases. Complexity, in turn, is guaranteed to increase given a stable and sufficient input of energy and as-yet unexplored molecular possibilities. The final step in preparing the biosphere for the emergence of life is the formation of the first metabolic cycles.

In his 68 text, Morowitz provided a proof for the following theorem:

     In steady state systems, the flow of energy through the system from a source to a sink will lead to at least one cycle in the system.

The proof is much too complicated to reproduce in this context, but we can understand the physical basis for this claim nevertheless. Let’s begin by returning to a materially closed system that can exchange light and heat with its surroundings but not mass. If this system is subjected to an energy gradient between a source and a sink, what are its available means of dissipating potential energy? First imagine a visible photon entering the system and being absorbed by an atom. This input energy will result in an electron being “promoted” to an excited state. The excited state has more potential energy than the ground state (the atom before absorbing the photon). This potential energy must dissipate somehow. The thing is, if the electron drops back to its ground state via exactly the reverse of the pathway that it took to get to the excited state, then the overall transformation is reversible and by definition this involves no dissipation (only irreversible processes produce entropy). In order for dissipation to occur the path to the high energy state must be different than path back to the lower energy state. But what I just described is a cycle. If you end up where you started via a different route than you left from, you have moved in a cycle. In order for energy to be dissipated by a materially closed system, at least one cycle must exist because this is simply the logically necessary condition for the perpetuation of an irreversible process in a closed system. As I’ve mentioned before, the biosphere as a whole is just such a materially closed system interposed between a stable energy gradient (sun and space). So this statement applies to the earth as a whole: In order for energy to flow, matter must cycle.

If we combine these last two ideas, that catalysis is the basis for non-equilibrium distributions of matter and that cycles are a necessary condition for dissipation in a closed system, we arrive at the idea the idea that the abiotic progenitors of living organisms were catalytic cycles. This is widely accepted in the origins literature but that doesn't mean that everyone agrees on why some type of catalytic cycle must have emerged before proper organisms or the emergence of a genetic code. In a future post we will contrast Eigen and Schuster's quasi-species theory with Jeffrey Wicken's proposed minimal autocatalytic cycle. Much of the debate hinges on whether one identifies energy processing or replication as the defining rationale of living organization. I'm sure you know which side I'm on, but before we can properly attack the gene-machine conception of organisms we need some more chemical details.

The raw material of molecular complexity produced through entropic randomization becomes information once a structure plays a catalytic role in a dissipative cycle. This is because henceforth, the molecule exists not because of its own thermodynamic stability or due to the randomizing tendencies of a system to produce new configurations, instead it exists because the cycle produces more entropy than the activity of the parts alone ever could. It is now part of a new thermodynamic whole which gains its identity by participation in a pattern of entropy production. Entropy production is thus the rationale which selects cycles over randomly distributed chemical transformations. Those cycles which produce the most entropy by definition also pull the most energy flux into themselves along with the most material resources.

Based on these considerations, we see that the thermodynamic view of evolution sees selection as operating well before the emergence of replication or the genetic code. Later on we will see that it also operates above the level of genes as well. This is because the second law operates at every level of the organic hierarchy, from the formation of atoms to flows of capital. Next time we will continue our discussion of catalytic cycles by introducing some simple concepts from information theory and discussing cycle selection in the context of pre-biotic evolution.

Thumbnail image is from here.