New Criticals

So last time I was discussing the second law and I explained it almost entirely in terms of “energetic” entropy, the dissipation of potential energy, which the earth’s biosphere produces by taking concentrated solar radiation (UV-visible light) and breaking it up into dilute, thermal radiation (heat). I used this example as my primary focus for several reasons. First, as I mentioned previously, the net conversion of light to heat is a precise measure of the overall entropy production of the earth. It is also usually NOT what people think about when they hear casual discussions of entropy. They think about “spontaneously increasing disorder,” which meshes nicely with our anthropocentric intuitions about the futility of our efforts in the face of time and the central moral creed of the 20th century: “The universe doesn’t give a damn about you.” Well the universe grew you, but whatever, it’s fun to feel heroic and unique using your powers of reason to bravely face the indifferent void.

At any rate while I’m going to continue to insist that entropy has absolutely nothing to do with disorder, mostly because I don’t know what disorder is even supposed to mean in a thermodynamic context, there is a perfectly valid concept known as “configurational entropy.” Configurational entropy refers to the range of energetically allowable material configurations a system possesses. So if the theme last week can be compressed as "Energy randomization," this week the theme is the operation of the second law on material possibility, "Matter randomization." Matter randomization is driven by the production of configurational entropy and it is also at the heart of most of the confused notions about entropy and disorder. Dispelling these confusions will hopefully also provide a clue as to why the second law promoted, rather than hindered, the increase in molecular variety that was critical to the emergence of life.

As I mentioned last time, all real, macroscopic processes increase the entropy of the universe and the way to quantify the entropy is to count the number of available arrangements of matter and energy in the system under consideration. We call a particular arrangement of matter and/or energy a “microstate” and the overall matter/energy content of our system a “macrostate.” Macrostates are characterized by average, macroscopic parameters like temperature, pressure, and volume. For a given system, like a fluid in a container, there will be a number of alternative “microscopic snapshots” consistent with a set temperature, pressure, or particle content--these are the microstates. A technical way of saying the second law is that a system spontaneously maximizes the number of microstates available to it. But first some mathematical and historical background. We use the variable “S” to represent entropy, and if we have a case which is simple enough that we can actually list all the possible microstates of the system, then we can calculate the entropy directly with the equation:

S = k*log(W)

This “microscopic” definition of entropy is due to Ludwig Boltzmann, and the equation is found on his tombstone in Vienna. The lowercase k is Boltzmann’s constant and it gives the right hand side the same units as entropy on the left: energy divided by temperature. I'm using an asterisk to indicate multiplication throughout this post. The log is just a log function and the W is the number of microstates. The thing to notice about the equation is that since k is a constant, the entropy only depends on the variable W, the number of microstates. That makes it sound easy but actually counting all of the microstates available to a real system is generally non-trivial. For people who like to hear the jargon, you have to “integrate over the entire phase space.” It can get messy. But before Boltzmann, entropy was only associated with the macroscopic meaning it has in classical thermodynamics.

In that case, call it the steam-engine view of reality, people had noted that if I want to take the potential for motion implied in having a hot thing (and thus a concentration of kinetic energy relative to the surroundings) and turn that potential into directed motion, like takin’ these folks and their stuff from Atlanta to New York on this train by burning this coal and boiling some water...well I can’t ever get all of the potential contained in the random motions of the hot thing and convert that into directed, or useful motion. So entropy was conceived as the “wasted energy” that attends any macroscopic process. But the universe ain’t no steam engine, and conservation (the first law) tells us that nothing is ever really lost. Furthermore, we know now that entropic sinks are as necessary for the perpetuation of complex life as are energy-dense fuel sources. So Boltzmann’s work was the first step in the liberation of thermodynamics from a strictly engineering paradigm into a coherent theory of all dynamic processes. One day soon I’ll do a post just about Boltzmann...he holds a very special place in my heart. For now just note that our ability to define entropy in terms of available microstates is due to him.

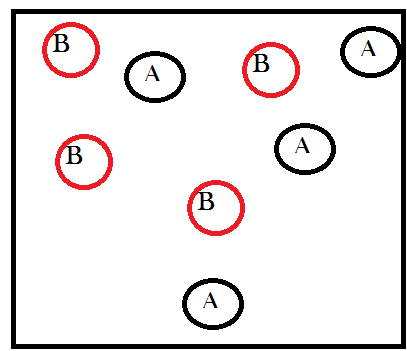
In order to understand matter-randomization, it is helpful to momentarily ignore energetic considerations and only think about the number of microstates available as a result of redistributions in the material content of a system, i.e. chemical reactions. So now let’s start with an abstract example that simplifies the mathematics as much as possible (this example comes straight from Wicken’s book that I mentioned before). Imagine a container that contains only 8 gas molecules of two different types: A and B. Imagine as well that there are equal amounts of both, four molecules of A and four molecules of B, like so:

With me so far?

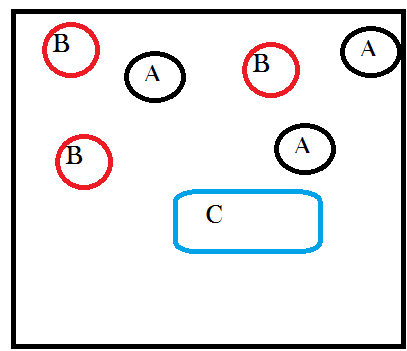
Next let’s give A and B the possibility, if they collide in just the right way, of joining together to form a new molecule that is a combination of A and B. We’ll call this new molecule “C” and we can write out the chemical reaction as:

A + B → C

A complicated reaction, I know. Ok so “ignoring energetic considerations” means assuming that the temperature and pressure in our container don’t change as a result of A and B combining to make C. This is an artificial assumption that I’m introducing so that we can analyze only the effects of matter transformations. Note that it takes two molecules, one each of A and B, to make one C. This means that every time this happens there is one less particle in our system because two things became one thing. But also the first time it happens there is one new particle in our system, a C exists where there were no C’s before. So after one reaction, our system will look like this:

See how I took away one A and oneB and replaced them with a new thing called C? Still with me?

Whatever composition results in the most microstates is what the system will spontaneously select. So we use the permutational equation to count the number of microstates available in a system:

Wc = N!/(N1!*N2!...*Ni!)

It’s really not that bad. Wc is the number of microstates, and the subscript C indicates that we are only examining the configurational possibilities (ignoring the energy contribution). The variable N is for the number of particles or items or whatever in your system, and the Ni in the denominator is how many of each kind of thing there are in the system, where i is a generic that ranges from 1 to however many different things you are analyzing. The ! is the factorial function which tells you how many different ways there are two arrange a set of things.

So for our super simple system that begins with four A’s and four B’s, N=8 because there are 8 total things and the denominator has two terms, Na=4 because there are four A’s and Nb=4 because there are four B’s. When we plug this information into the formula above, it becomes:

Wc = N!/(Na!*Nb!) = 8!/(4!*4!) = 40,320/576 = 70

In written language then, there are 70 ways to permute 4 of one kind of thing and four of another kind of thing. Ok but what about for the second state after the reaction has taken place once, and there are three A’s, three B’s, and one C? Well now N=7 and the denominator has three terms, Na, Nb, and Nc, for the number of molecules of type A, B, and C respectively. Putting this into the permutational equation we get:

Wc = N!/(Na!*Nb!*Nc!) = 7!/(3!*3!*1!) = 5,040/36 = 140

Do you see what happened mathematically? The numerator got much smaller when the particle number changed from 8 to 7 but the denominator decreased faster as a result of a new thing being put into the system. Dividing by a small number is the same as multiplying by a big number and so the overall number of possible microstates increases as a result of the reaction. When the microstates increase the configurational entropy increases as well and so the second law will promote the spontaneous formation of a new molecule of C.

We can generalize this result further by imagining a new parameter called the “extent of reaction.” In the example where one begins with four A’s and four B’s then the reaction A + B → C can happen, at most, four times. The least it can happen is zero times. In a more realistic scenario there would be something like 10^26 molecules in your system and the reaction might occur or not many times. So we graph the extent of reaction as a percent of the total times the reaction can possibly occur and let it range between 0 and 100. You can take the W number calculated from the permutational equation for each time the reaction might occur and stick it into Boltzmann’s entropy formula, S = k*log(W), and then graph the entropy S as function of how many times the reaction has occurred, with the “extent of reaction” parameter on the x-axis and configurational entropy on the y-axis. You get something that looks like this:

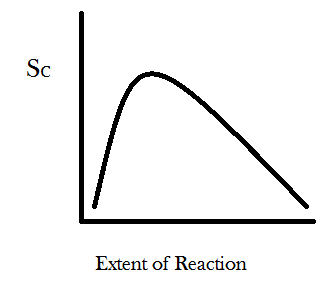For the simple reaction A + B → C the entropy is maximized at about 29% completion. For different reactions with different ratios of reactants to products the configurational entropy will be maximized at different percents of completion. Also keep in mind that the systems true equilibrium (maximum entropy) can only be found by taking into account the change in the number of energetic microstates as well. The point  I would like you to take away from this graph is that the slope of the curve is always positive for small values of the extent of reaction and always negative for large values. The physical meaning of these asymptotic slopes is that matter-randomization considerations promote all chemical transformations through some compositional range. Undergraduate chemistry students are taught this lesson as a particular instance of “Le Chatelier’s Principle.”

One way of explaining this principle of chemical reactions is saying that if you build up a large enough concentration of one kind of thing in one place, even energetically unfavorable processes will start to occur spontaneously as a way of equalizing this improbability in the distribution of matter. Crucially for evolution, these considerations always promote the formation of something new, although how much of the new thing gets made will depend upon the energetics of the process (this basically amounts to how much heat the reaction gives off or requires).

Matter-randomization is also the basis for “Murphy’s law,” the unofficial, cynical corollary of the second law. Do we see now that the real issue isn’t that "whatever can go wrong will go wrong," but rather that thermodynamics guarantees that anything that can happen must happen to some extent. Conversely, no chemical process ever proceeds entirely to completion. That's because what's true for the forward reaction is also true for the back reaction. Or just imagine that we start off our previous example with a container holding only four molecules of "C." We'd be starting on the far right side of the above graph. The way to increase the microstates from this initial state is to have C's break apart back into A's and B's.  These assertions requires strong qualification though.

Thermodynamics is principally concerned with energy flows and energetic barriers to reactions may prevent them from occurring for periods longer than the age of the universe, which may as well be the same as saying they never happen. Additionally, thermodynamics says nothing about whether or not two things can undergo a chemical reaction or not. For this, you need to know some structural details about the actual chemicals; so you can't talk about an abstract chemical reaction between "A" and "B" anymore, you have to talk about real compounds like water or oxygen. Such considerations, however, provide a more solid thermodynamic foundation to the clear utility of carbon-based molecules for life.

No other element really even comes close to carbon in terms of the diversity of possible structures it can form. Life on earth has been busy creating a wider and wider variey of organic molecules for the past 4 billion years, and there's no evidence yet that it has even scratched the surface of the variety of organic molecules that might be possible (to a chemist "organic" just means "has carbon in it"). So once the randomizing directives of the second law found an endless playground in the structural possibilities of carbon molecules, all it needed was a sustained energy flux through a materially closed system (provided by the sun, earth, and our mother the expanding sink of space) to begin generating actual variety out of these configurational possibilities.

A few of the endless possibilities you get with Carbon...

Ok so to summarize the statistical presentation of the second law's teleological directive to randomize matter: Anytime you concentrate a great many of the same thing in one place, you put pressure on a system to come up with ways to rearrange that thing into something new and thereby increase the configurational possibilities of the universe. Again then, we see that the production of entropy is only tangentially connected to the wasted effort given off by our motors and is rather the explanation for the statistical drive that ensures the immanent differentiation and ceaseless mixing of the biosphere. As space itself expands due to the fact that we live after the big bang, so too do the historical possibilities of a complex system increase with time. I have come to be convinced that these phenomena are fundamentally connected and will one day provide deep insight into the structure of time and physical nature, though I have no idea yet what that realization might be…

So that’s matter randomization and configurational entropy. Next time we’ll connect matter and energy flows through the concept of chemical cycles which were the abiotic progenitors of life on this planet. Stay tuned!

Thumbnail image